基于FPGA的图像形态学膨胀算法实现,包括tb测试文件和MATLAB辅助验证

目录

1.算法运行效果图预览

2.算法运行软件版本

3.部分核心程序

4.算法理论概述

5.算法完整程序工程

---

1.算法运行效果图预览

在FPGA中仿真结果如下所示：

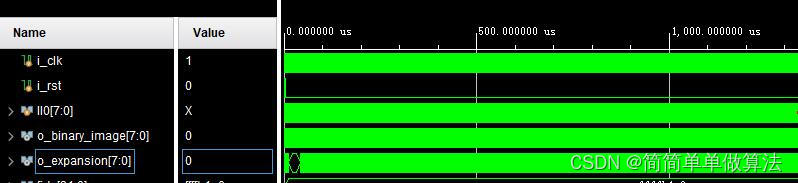
将FPGA中的仿真结果导入到matlab显示二维图，效果如下：

2.算法运行软件版本

matlab2022a

vivado2019.2

3.部分核心程序

`timescale 1ns / 1ps
//
// Company: 
// Engineer: 
// 
// Create Date: 2022/07/28 01:51:45
// Design Name: 
// Module Name: test_image
// Project Name: 
// Target Devices: 
// Tool Versions: 
// Description: 
// 
// Dependencies: 
// 
// Revision:
// Revision 0.01 - File Created
// Additional Comments:
// 
//


module test_image;

reg i_clk;
reg i_rst;
reg [7:0] image_buff [0:100000];
reg [7:0] II0;
wire [7:0] o_binary_image;
wire [7:0] o_expansion;
integer fids,jj=0,dat;
........................................................................
 
initial 
begin
i_clk=1;
i_rst=1;
#2000;
i_rst=0;
end 

always #10  i_clk=~i_clk;
 
always@(posedge i_clk) 
begin
	II0<=image_buff[jj];
	jj<=jj+1;
end
 
 
tops tops_u(
.i_clk              (i_clk),
.i_rst              (i_rst),
.i_I0               (II0),
.o_binary_image     (o_binary_image),
.o_expansion        (o_expansion)
);

integer fout1;
integer fout2;
initial begin
  fout1 = $fopen("binary_image.txt","w");
  fout2 = $fopen("expansion.txt","w");
end

 
always @ (posedge i_clk)
 begin

	$fwrite(fout1,"%d\n",o_binary_image);
	$fwrite(fout2,"%d\n",o_expansion);
end

endmodule
0X_012m

4.算法理论概述

       膨胀操作是形态学中另外一种基本的操作。膨胀操作和腐蚀操作的作用是相反的，膨胀操作能对图像的边界进行扩张。膨胀操作将与当前对象（前景）接触到的背景点合并到当前对象内，从而实现将图像的边界点向外扩张。如果图像内两个对象的距离较近，那么在膨胀的过程中，两个对象可能会连通在一起。膨胀操作对填补图像分割后图像内所存在的空白相当有帮助。二值图像的膨胀示例如图所示。

       在膨胀过程中，也是使用一个结构元来逐个像素地扫描要被膨胀的图像，并根据结构元和待膨胀图像的关系来确定膨胀结果。

         基于FPGA的图像形态学膨胀算法实现主要依赖于图像处理的基本原理和数学形态学的基础知识。在图像处理中，形态学操作被广泛应用于各种图像处理任务，包括噪声消除、对象检测和识别、图像分割等。其中，膨胀操作是形态学操作的一种基本形式，它有助于增加图像中明亮区域的大小。

        首先，让我们了解一下图像形态学的基础知识。形态学操作通常在二值图像上进行，但是也可以扩展到灰度图像和彩色图像。在二值图像中，形态学膨胀操作被定义为将一个结构元素（通常是一个小的矩形或圆形）在图像上移动，并将每个像素值替换为该像素值和结构元素中心值的最大值。这样，在经过膨胀操作后，图像中的明亮区域（或高像素值区域）会得到增强。

具体来说，膨胀操作的数学表达式可以表示为：

Dilation(f,I)=max⁡{f(x−s),I(x)+s}(x)f(x−s)+I(x+s)​max{f(x-s), I(x+s)}

        其中，f是原始图像，I是结构元素，s是结构元素的位移。这个公式表示的是，对于每一个像素位置x，将结构元素中心对齐到位置x-s，并取结构元素覆盖区域的最大值作为输出图像在该位置的值。

        在FPGA上实现图像形态学膨胀算法时，可以采用硬件并行处理的方式，以提高处理速度。首先，将输入的图像数据存储在FPGA的内部寄存器中。然后，通过一个并行处理器，将结构元素在图像上移动，并计算每个像素位置的输出值。

        需要注意的是，在实现形态学膨胀算法时，需要选择合适的结构元素形状和大小。不同的结构元素可能会导致不同的膨胀效果。此外，由于形态学操作涉及到大量的数据运算，因此需要合理优化算法和硬件设计，以提高处理速度和效率。

       总的来说，基于FPGA的图像形态学膨胀算法实现需要结合图像处理的基本原理和数学形态学的基础知识，同时考虑硬件并行处理的特点和实际应用的需求。通过合理选择结构元素、优化算法和硬件设计等手段，可以实现高效的图像膨胀操作。

5.算法完整程序工程

OOOOO

OOO

O